Klimawandel in Europa
Contents
Einleitung
Die Beobachtungen der letzten Jahrzehnte haben gezeigt, dass sich das Klima verändert. Globale Erwärmung, saurer Regen und das Ozonloch sind unsere größten Umweltbedrohungen. Dies hat zum Abschmelzen der Gletscher, zu häufigen Extremwetterereignissen, zum Rückgang der Nahrungsmittelproduktion, zum Anstieg des Meeresspiegels und zum Aussterben von Arten geführt. Der Klimawandel hat negative Auswirkungen auf terrestrische und marine Ökosysteme und die Gesundheit. Die Niederschläge, ein wichtiges Element des Klimas, haben sich ebenfalls verändert. Zwischen 1901 und 2003 kam es zu einer Zunahme der extremen Niederschläge, während es in Europa in Nordeuropa mehr und im Mittelmeerraum weniger regnete (Bates et al., 2008).
Veränderung in der Niederschlagsmenge können von verschiedenen Faktoren abhängen. Die Niederschlagsmenge hängt in hohem Maße von der Temperatur und den Wetterbedingungen ab. In trockenen Gebieten können hohe Temperaturen den Boden schneller austrocknen und die Temperaturen erhöhen, während hohe Temperaturen in feuchten Gebieten die Niederschläge erhöhen können, indem sie die Wasserverdunstung beschleunigen. Gleichzeitig können El Niño und die Nordatlantische Oszillation (NAO) auch die Intensität und Verteilung der Niederschläge beeinflussen und einige Gebiete trockener und andere feuchter machen (Bates et al., 2008). Der NAO-Index für die NAO gibt die Differenz der Druckabweichung an der Station in Ponta Delgada und Stykkishólmur an. Wenn er positiv ist, nehmen die Niederschläge in Nordeuropa zu und an der Mittelmeerküste ab. Wenn er negativ ist, nehmen die Niederschläge in Nordeuropa ab und die Niederschläge im Mittelmeerraum zu (Dahlman, 2009).
Die Veränderung des Niederschlagsregimes in Europa in den letzten Jahrzehnten könnte mit Biomen zusammenhängen. So wurde die durchschnittliche Veränderung im Niederschlagsregime für jedes Biome in Europa zwischen den beiden Perioden: 1962 bis 1970 und 2010 bis 2018 berechnet und die Veränderung der Niederschläge in ganz Europa interpoliert. Die Risikobereiche, in denen der Niederschlag um mehr als 5 % zu- oder abnimmt, wurden ermittelt.
Daten und Methoden
Daten
Im Zuge dieser Übung wurden Software r (Version 4.0.5) und R-Pakete gstat_2.0-7, rgdal_1.5-23, dplyr_1.0.6, tmap_3.3-2, raster_3.4-10, und sp_1.4-5 verwendet (Siehe Anhang für den vollständigen Code).Der in der Übung verwendete Datensatz KlimaStatEuropa_Niedersschlaege enthält die durchschnittliche jährliche Niederschlagsmenge (mm, Mittelwert, Standardabweichung) für zwei Zeiträume: 1962 bis 1970 und 2010 bis 2018 mit den Koordinaten der Längen- und Breitengrade im WSG 84. Die durchschnittliche jährliche Niederschlagsmenge in den europäischen Klimastationen von 1962 bis 1970 schwankt zwischen 145 mm und 2590 mm. Im Gegensatz dazu lag die durchschnittliche jährliche Niederschlagsverteilung von 2010 bis 2018 zwischen 132 mm und 2792 mm. Ihre räumliche Verteilung ist in Abbildung 1dargestellt.
Die Biome_Europa Shape-Datei enthält Daten über die Biome Europas, die in neun Kategorien unterteilt sind. Die Hauptkategorien sind Tundra für die nördlichsten skandinavischen Gebirge, Taiga/Forests für Nordeuropa, Temperate Broadleaf & Mixed Forests in Mitteleuropa, Mediterranean Forests, Woodlands & Scrub für die südliche Mittelmeerküste, Temperate Grassland, Savannas & Shrublands für das Schwarzmeertiefland und Temperate Conifer Forests in den Alpen, den Karpaten und den schottischen Highlands.
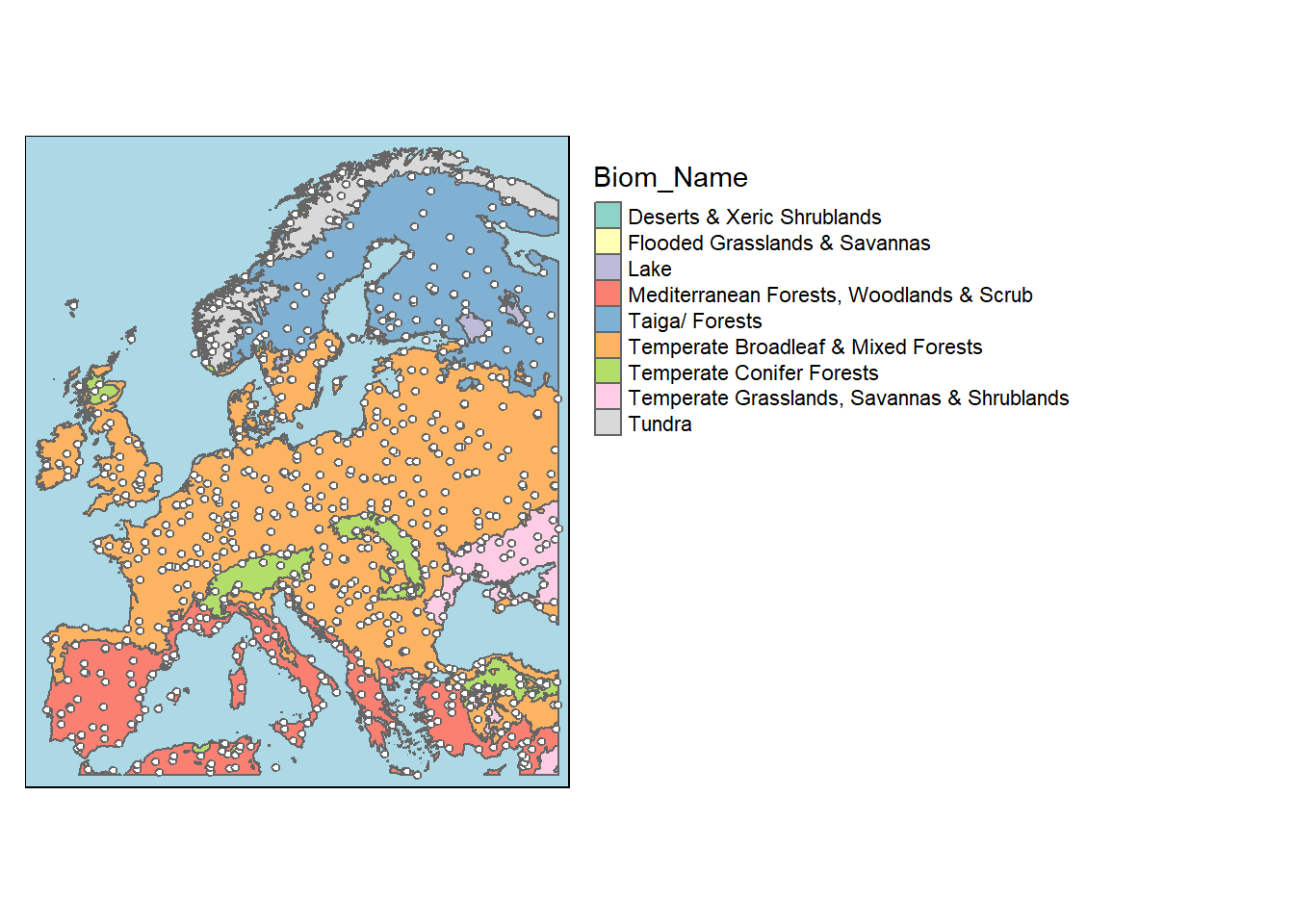
Figure 1: In der übung verwendete Daten: Verteilung der Biome und Klimastationen in Europa. Die weissen Punkte sind die Standorte der Klimastationen.
Niederschlagsveränderungen für Biomen
Die Differenz des Jahresniederschlags zwischen den beiden Perioden wurde zur Berechnung der Niederschlagsänderung für jede Klimastation verwendet. Die absolute Veränderung wird durch die Niederschlagsmenge von Periode 1 (1962 bis 1970) geteilt, um die relative Veränderung der Niederschlagsmenge zu erhalten.
Nach der Konvertierung des Datensatzes KlimaStatEuropa_NiedersschlaegeErgebnisse in sp-Objekt wurde die durchschnittliche Veränderung im Niederschlagsregime für jedes Biome in Europa in r mit dem Befehl aggregate im sp-Paket berechnet.
Interpolation mit Hilfe von Kriging
Bei der Interpolation wird die Kriging-Methode angewandt, bei der die Werte von Gebieten, für die keine Daten vorliegen, mit Hilfe eines Variogramm-Modells vorhergesagt werden. Das Variogramm-Modell beschreibt den Zusammenhang zwischen dem Abstand eines Punktpaares und seiner Varianz der Differenz. Ein lineares Trendmodell wird unter Verwendung des Längen- und Breitengrades der Klimastationen als unabhängige Variablen erstellt, um trendbereinigte Daten zu erhalten. Und dann mit Hilfe einer Variogramm-Analyse wurden die Daten untersucht. Die mittleren Variogrammwerte wurden mit der Funktion variogram in Package gstat berechnet und mit vier Modellen: lineares Modell, sphärisches Modell, exponentielles Modell und Gauß Modell angepasst. Die vier Modelle wurden verglichen und das Modell mit dem geringsten Fehler wurde als endgültiges Variogramm-Modell für Kriging verwendet.
Der Risikobereich wird nach der Indikator-Kriging-Methode berechnet. Das gleiche Trendmodell wie beim letzten Abschnitt wurde genommen, um den Bereichen zu berechnen, bei denen die relative Zu- bzw. Abnahme der Jahresniederschlag größer oder gleich 5% ist. Variogramm-Schätzer wurde auch von den linearen, sphärischen, exponentiellen und Gauß’schen Modelle angepasst. Das beste Modell wurde für Kriging übriggelassen.
Ergebnisse
Um die Veränderungen im Niederschlagsregime in Europa in den letzten Jahrzehnten zu ermitteln,wurden die absolute und relative Veränderung der mittleren Jahrensniederschaläge zwischen den beiden Perioden 1962 bis 1970 und 2010 bis 2018 für die einzelnen Klimastationen berechnet und kartografisch dargestellt. Im Norden Europas nahmen die Niederschläge zu, vor allem in mehreren Klimastationen im Nordwesten, wo die Niederschläge um mehr als 300 mm zunahmen und die relative Niederschlag 10% überstieg (Abbildung 2). Während im Süden Europas die Niederschläge abnahmen, und zwar in mehr als 10 Klimastationen um mehr als 100 mm. Der größte Rückgang der relativen Veränderung fand in einer der südwestlichen Klimastationen statt, mit einem Rückgang von mehr als 20%. Insgesamt haben die Niederschläge in Europa zwischen 1962 und 2018 im Norden zu- und im Süden abgenommen.
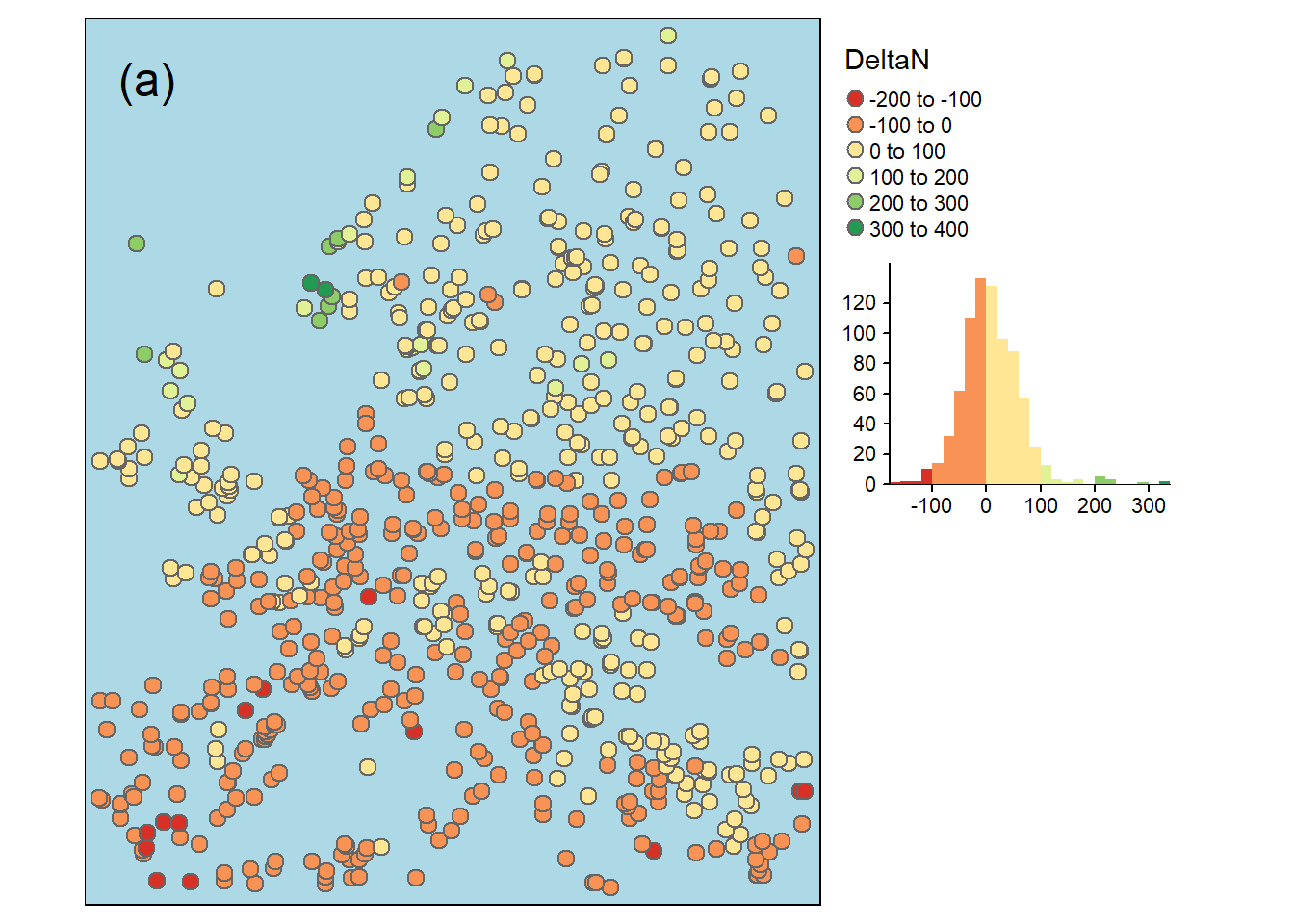
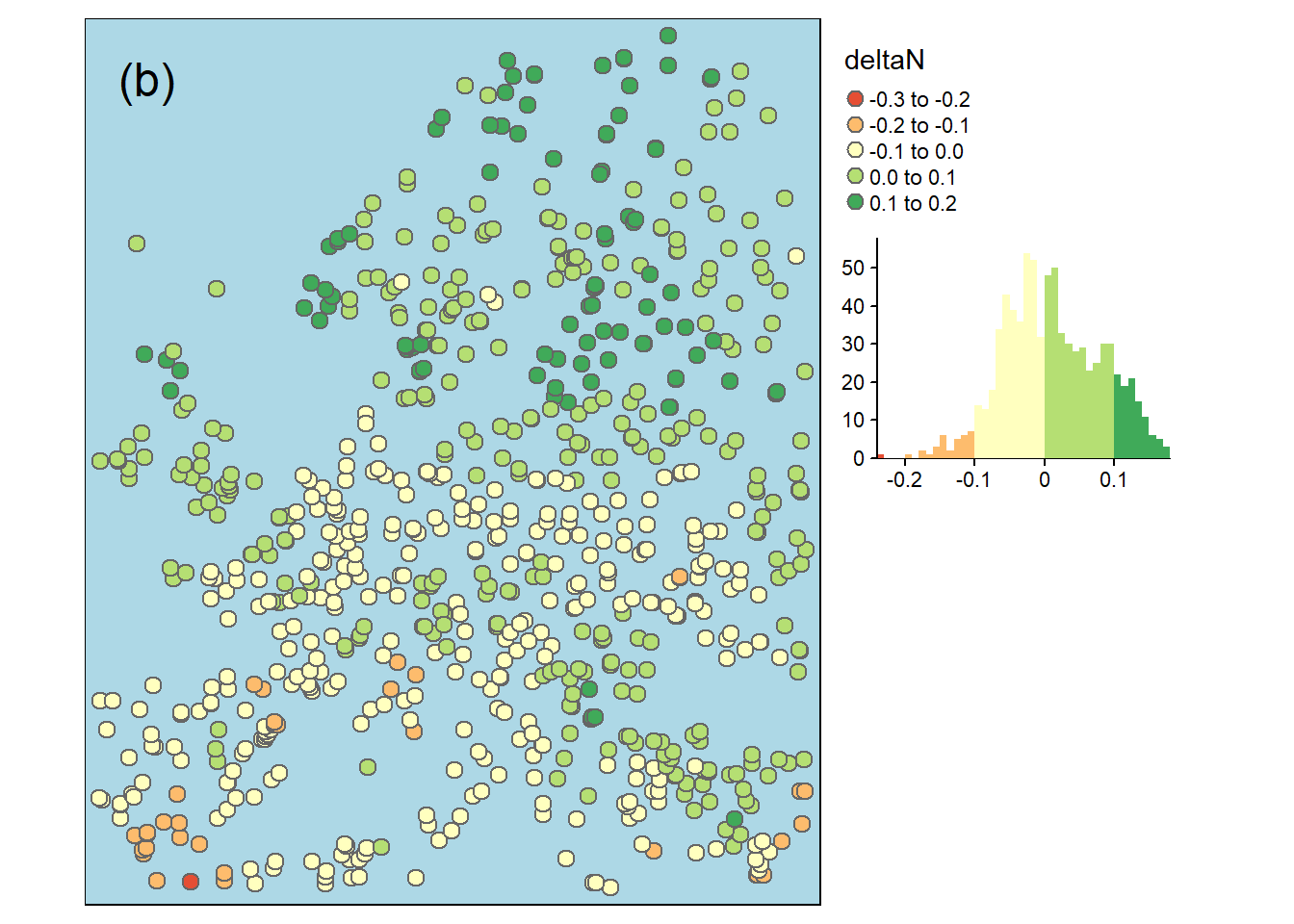
Figure 2: Absolute (a) und relative (b) Veraenderung der mittleren Jahresniederschlaege an europaeischen Klimastationen zwischen den beiden Perioden 1962 bis 1970 und 2010 bis 2018.
Um den Zusammenhang zwischen Niederschlagsveränderungen in den letzten Jahrzehnten und Biom in Europa zu verdeutlichen, wurde die Veränderung des durchschnittlichen Jahresniederschlags mit Hilfe von Balkendiagrammen und Karten für jedes Biom dargestellt. Das Gebiet mit der höchsten Niederschlagszunahme liegt in der Tundra in Nordeuropa, mit mehr als 100 mm und einer durchschnittlichen Zunahme der Niederschläge um mehr als 10 % (Abbildung 3). Die Wälder Mitteleuropas weisen ebenfalls eine Zunahme von 0-50 mm auf, wobei die relative Zunahme weniger als 10 % beträgt. Im Gegensatz dazu verzeichneten Mediterranean Forests, Woodlands & Scrub und Temperate Grasslands, Savannas & Shrublands im Süden einen Rückgang der Niederschläge. Das Temperate Grasslands, Savannas & Shrublands verzeichnete einen Rückgang der Niederschläge um 3 %, während die mediterranen Wälder einen Rückgang von über 20 mm verzeichneten, was einem relativen Rückgang von über 5 % entspricht.
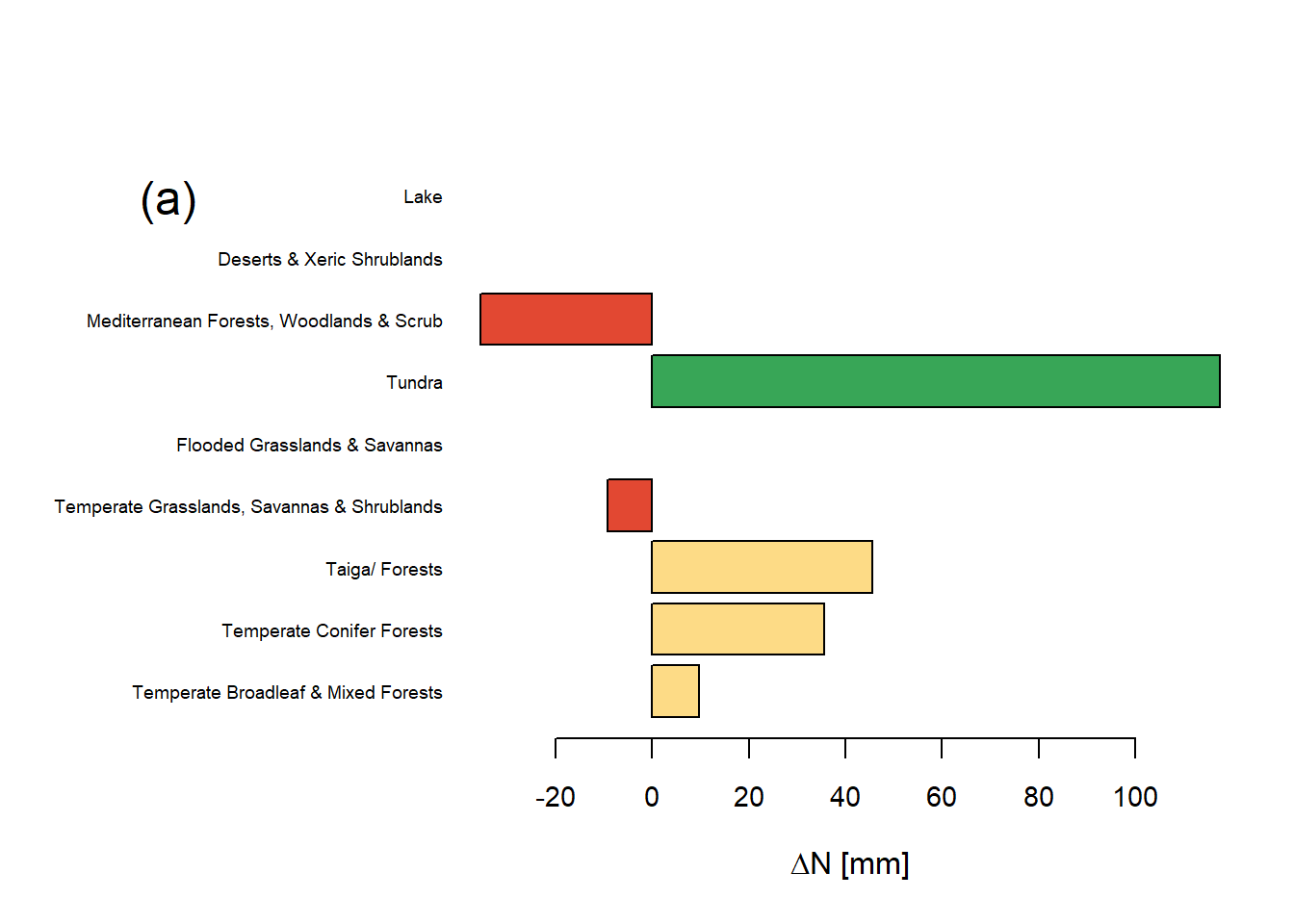
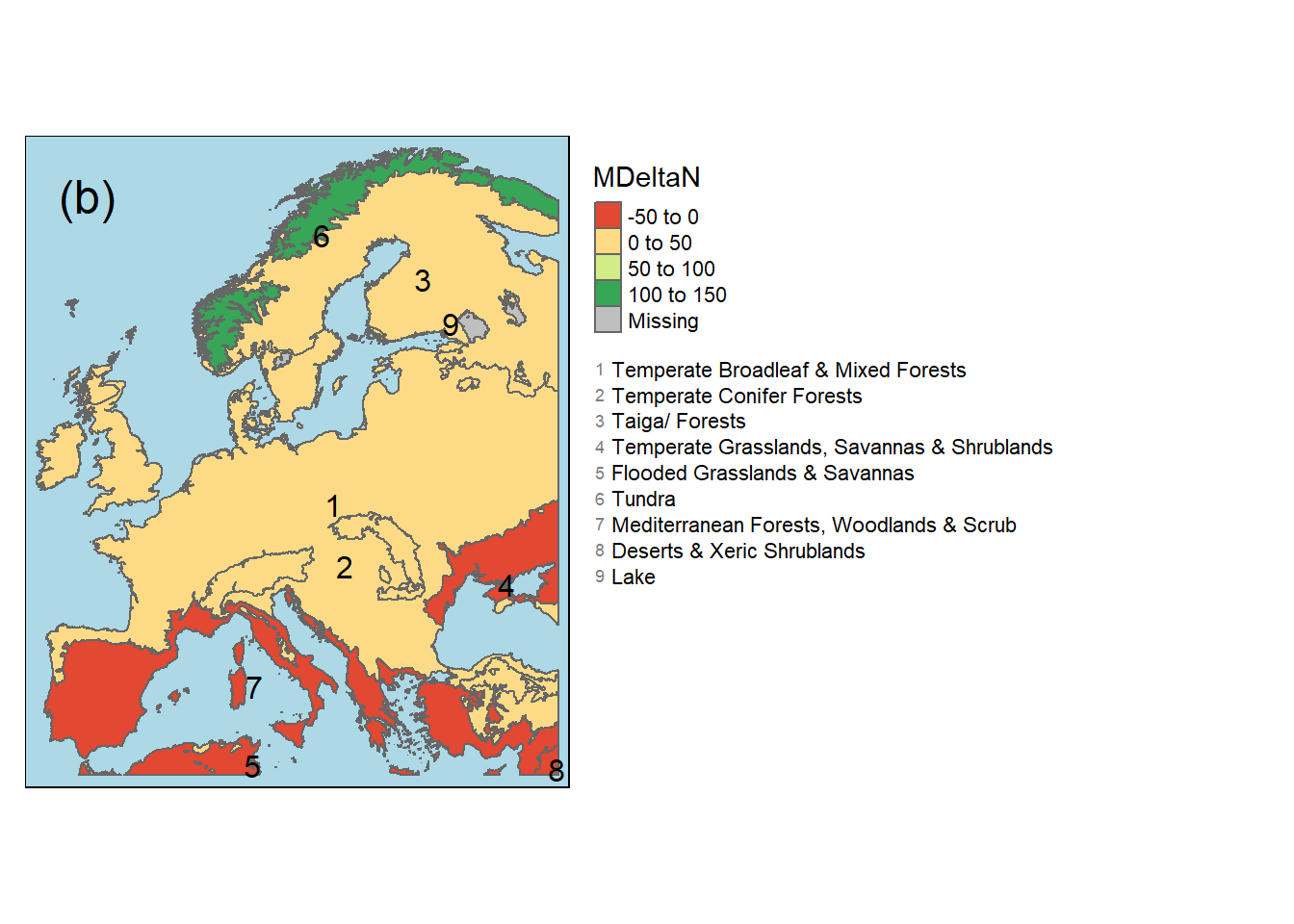
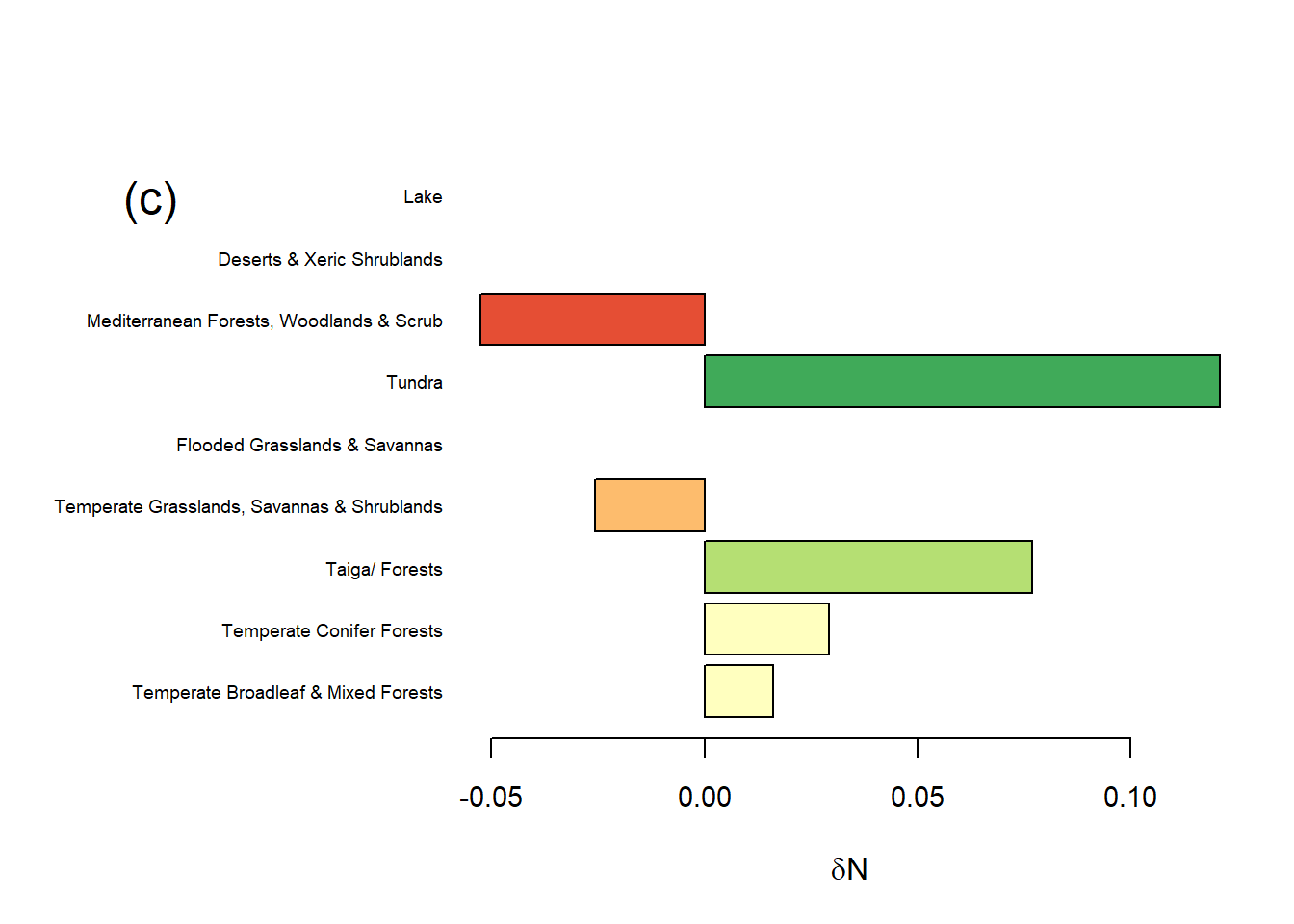
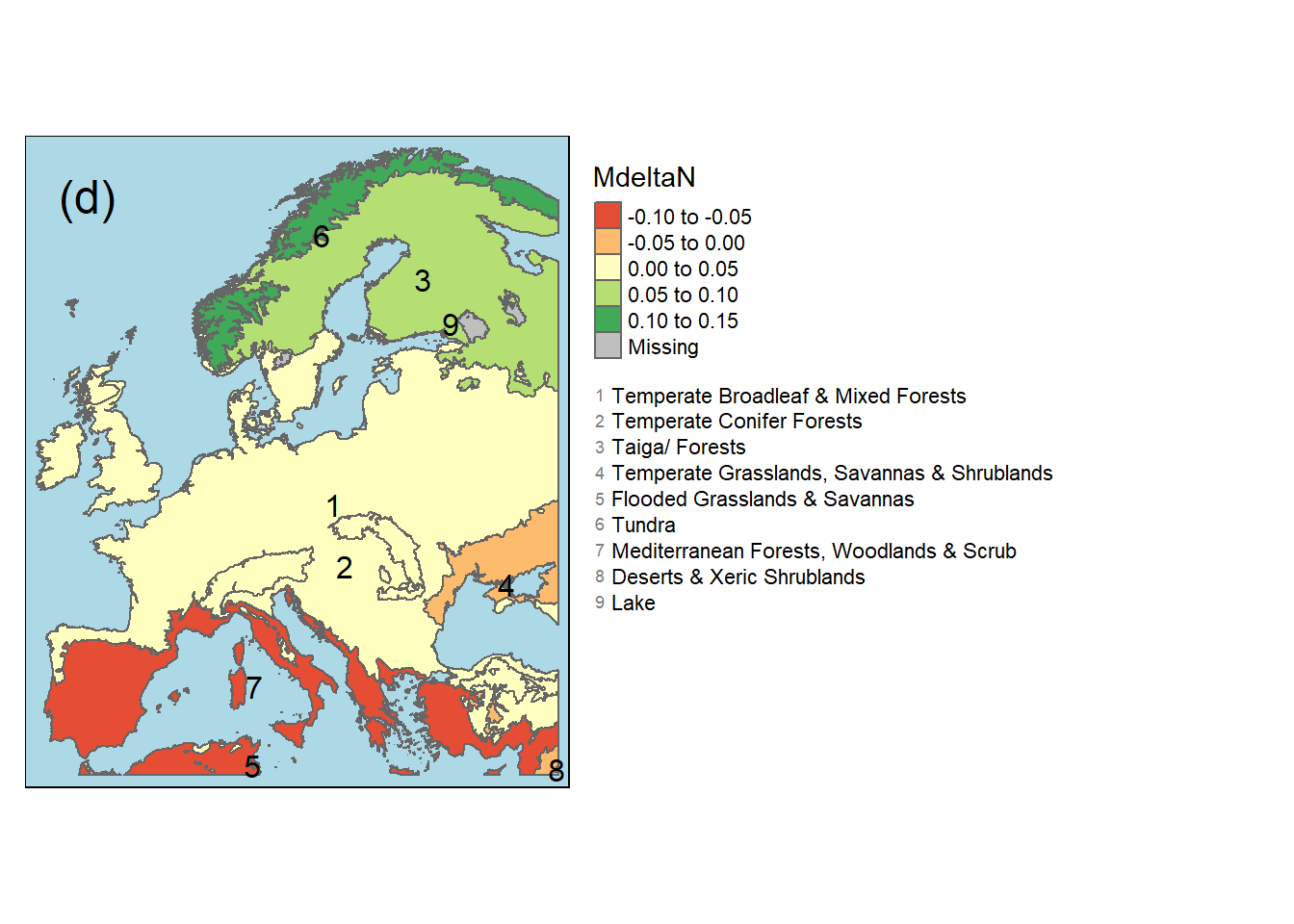
Figure 3: Absolute (a,b) und relative (c,d) Veraenderung der mittleren Jahresniederschlaege für die europaeischen Biomen zwischen den beiden Perioden 1962 und 1970 und 2010 bis 2018.
Zur Erstellung des Variogramm-Modells, und den Zusammenhang zwischen der Veränderung des Niederschlags und der Entfernung von Klimastationen bestimmt, wurde ein lineares Modell mit lon, lat als unabhängigen Variablen aufgestellt und vereinfacht, indem die unabhängige Variable mit unbedeutender Korrelation entfernt. Die relative Veränderung des Niederschlags in Abhängigkeit von den Koordinaten vorhergesagt wurde. Die sich daraus ergebende Gleichung lautet:
wobei deltaN die relative Änderung des Niederschlags, x die Länge der geografischen Koordinaten und y die Breite der geografischen Koordinaten ist.
Um das Variogramm-Modell auszuwählen, das am besten zum Variogramm-Schätzer bei der Interpolation passen, wurden die Fehler der linearen, sphärischen, exponentiellen und Gauß’schen Modelle verglichen. Das Gauß-Modell ist das Modell mit dem kleinsten Fehler und wurde für Kriging verwendet. Das Modell hat ein Nugget von \(6\cdot10^{-5}\), einen Sill von 0,003 und einen Practical range von 536.
Die relativen Veränderungen des Niederschlags über ganz Europa (Schätzer und Fehler) wurden mit Hilfe der Kriging-Methode interpoliert. In Übereinstimmung mit den Originaldaten nimmt der Niederschlag im Norden tendenziell zu und im Süden ab (Abbildung 4). Der Vorhersagekarte zufolge sind die größten Zuwächse vor allem in den Ländern Lettland, Estland und Litauen an der Ostküste der Ostsee zu verzeichnen, mit einem Anstieg von etwa 20 %. Der stärkste Niederschlagsrückgang ist in Spanien im Süden zu verzeichnen, mit einer Abnahme von etwa 25 %. Deutschland in Mitteleuropa und die Nordwestküste des Schwarzen Meeres um Moldawien und die Ukraine sind ebenfalls Gebiete, in denen die Niederschläge stärker zurückgegangen sind, nämlich um etwa 10 %. Die Fehler in den Daten sind insgesamt sehr gering (unter 0,0016) und sind vor allem an den Rändern der Karte größer.
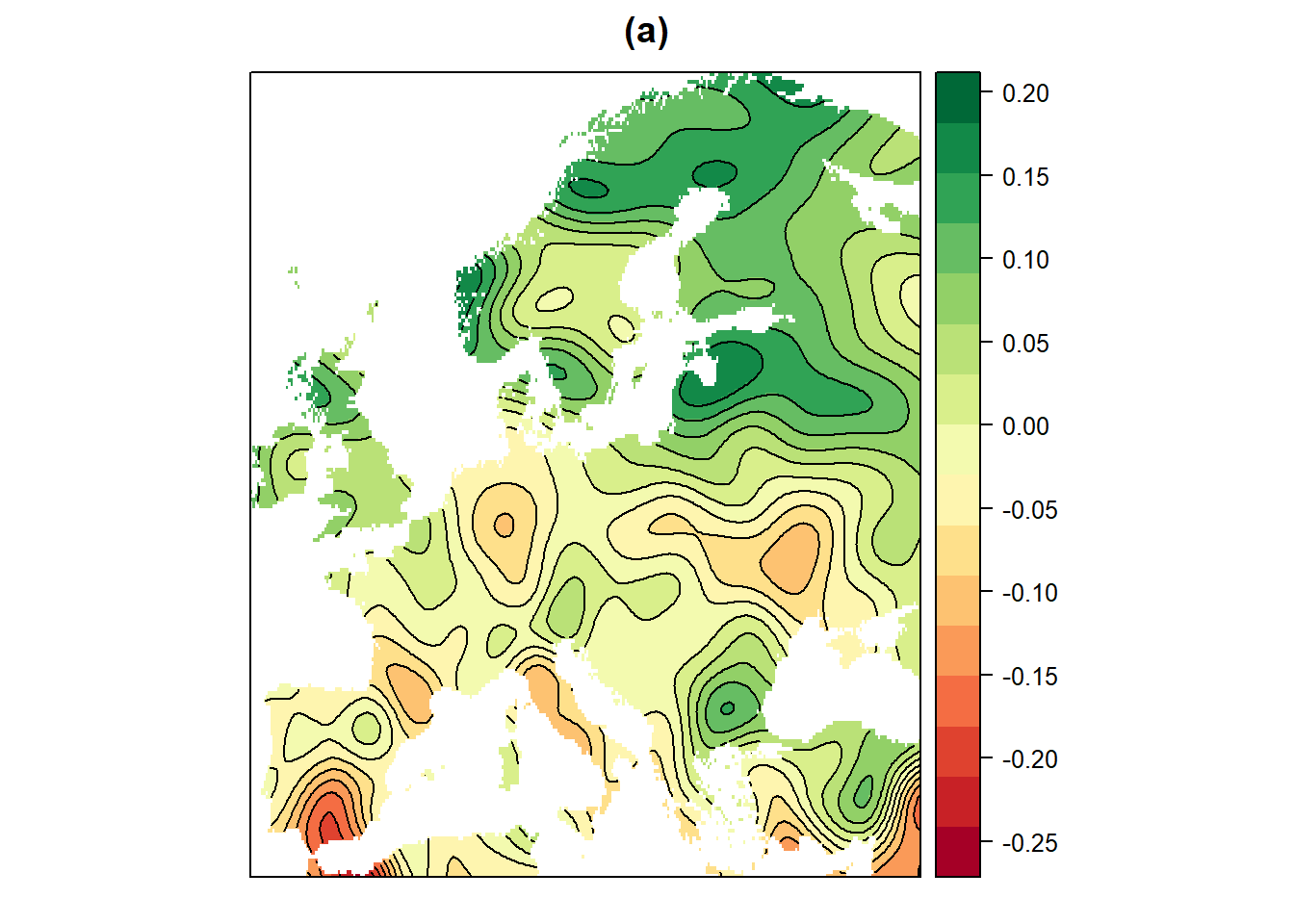
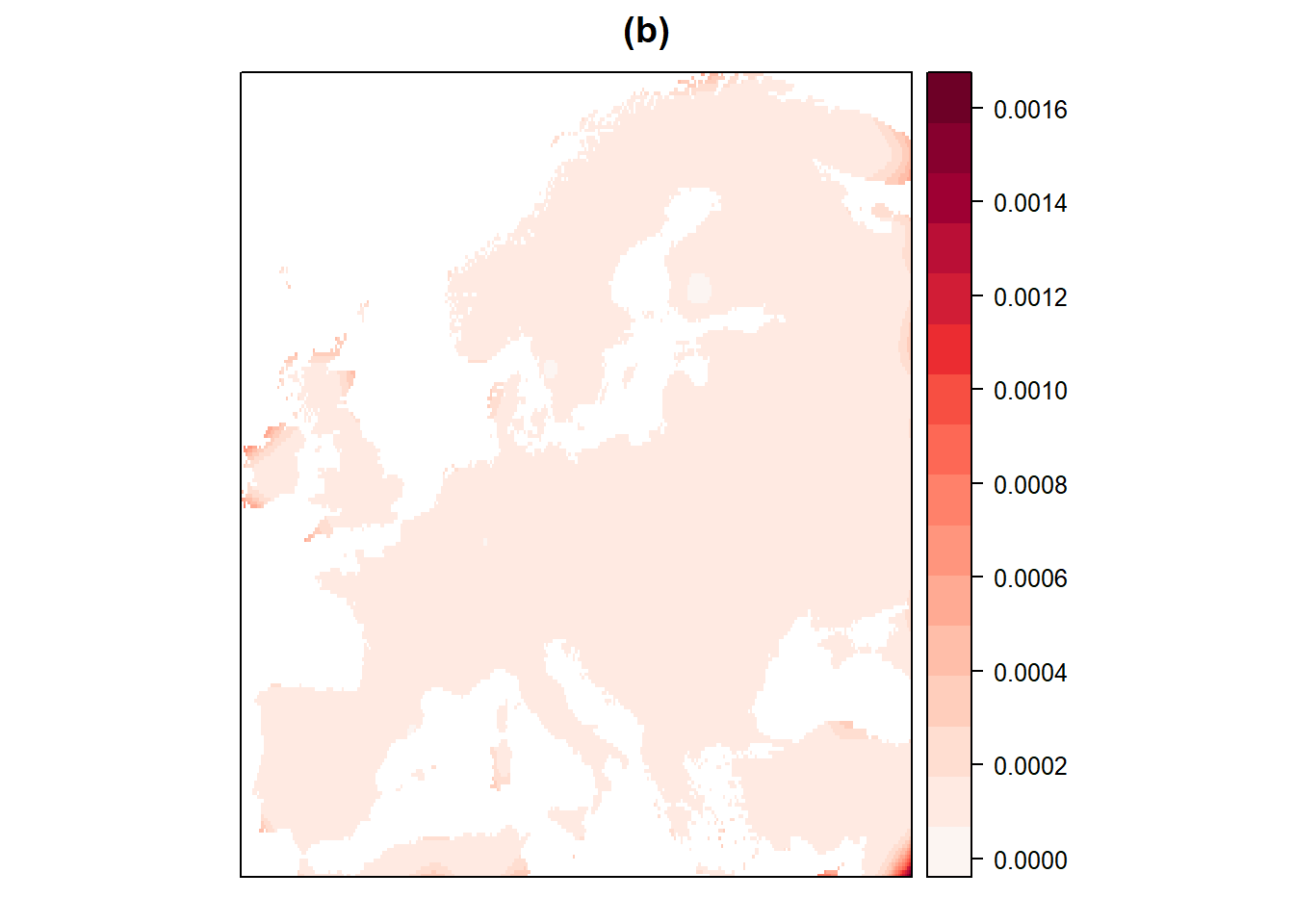
Figure 4: Schaetzer (a) und Fehler (b) der Interpolation von europaeischen relativen Niederschlagsveraenderungen mit Hilfe von Kriging und dem Gau<U+00DF>schen Variogramm-Modell
Um zu erfahren, welche Regionen von der Veränderung der Niederschlagsregime besonders betroffen sind, wurden die Regionen, die das “Risiko” einer relativen Zu- bzw. Abnahme der Jahresniederschläge um >= 5 % dargestellt. Die verschiedenen Variogramm-Modelle werden ebenfalls verglichen und sphärisch ist das beste Modell sowohl für Variogramm mit einer Niederschlagszunahme von mehr als 5% als auch für Variogramm mit einer Abnahme von mehr als 5%. Die Risikogebiete mit erhöhten Niederschlägen konzentrieren sich hauptsächlich auf Nordeuropa, vor allem auf Skandinavien im Norden, die baltischen Staaten und Westrussland, die Insel Irland, die Insel Großbritannien und den Südwesten des Schwarzen Meeres sowie auf die Ausläufer der Südostseite der Alpen (Abbildung 5). Das Risiko geringerer Niederschläge konzentriert sich auf den südlichen Teil der Iberischen Halbinsel, wo Spanien liegt, auf die Pyrenäen und das Aquitanische Becken im Norden, auf die italienische Halbinsel, auf Deutschland und auf das Tiefland am nordwestlichen Schwarzen Meer. Der Fehler bei der Zu- und Abnahme des Jahresniederschlags liegt im Wesentlichen unter 0,05.
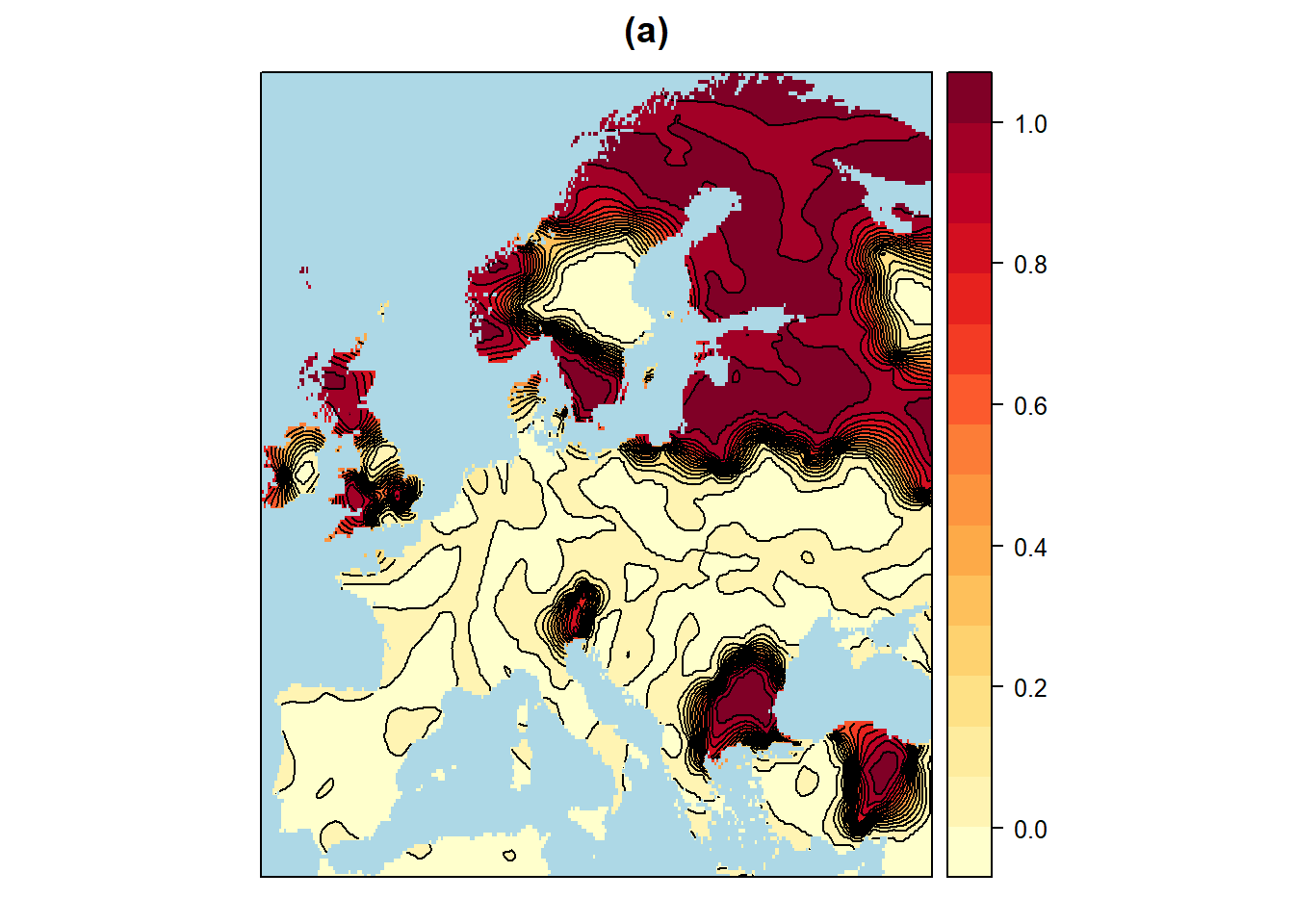
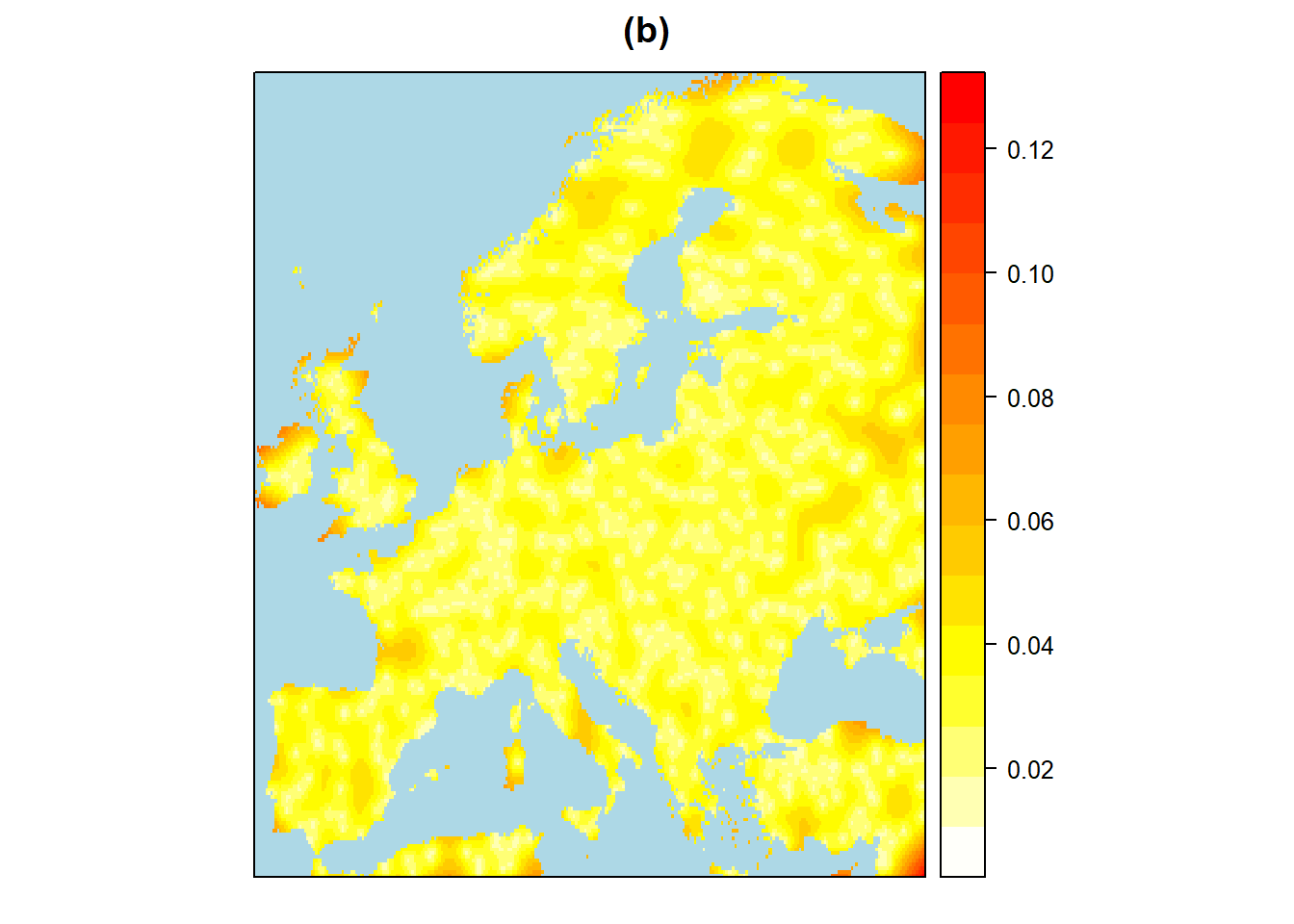
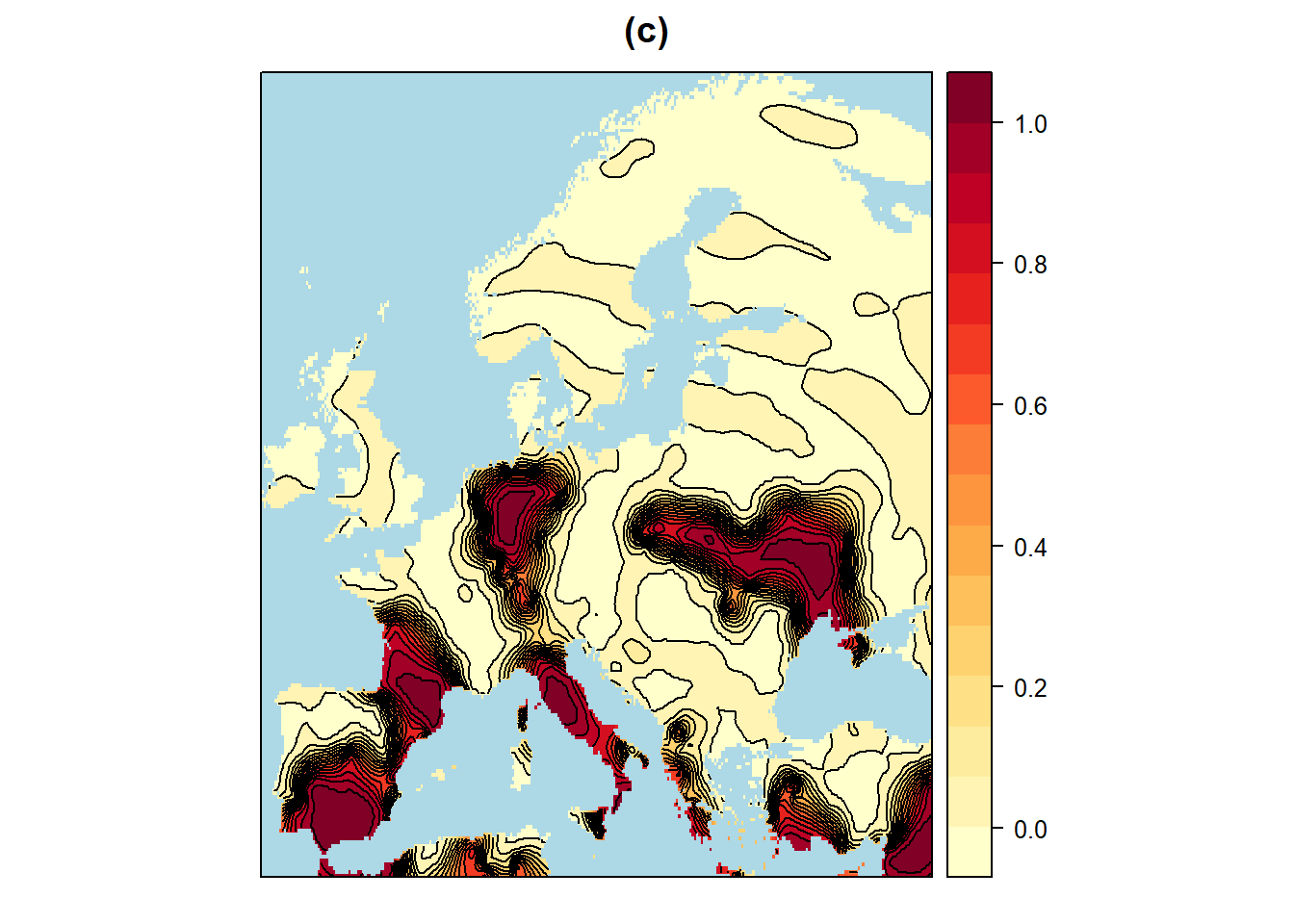
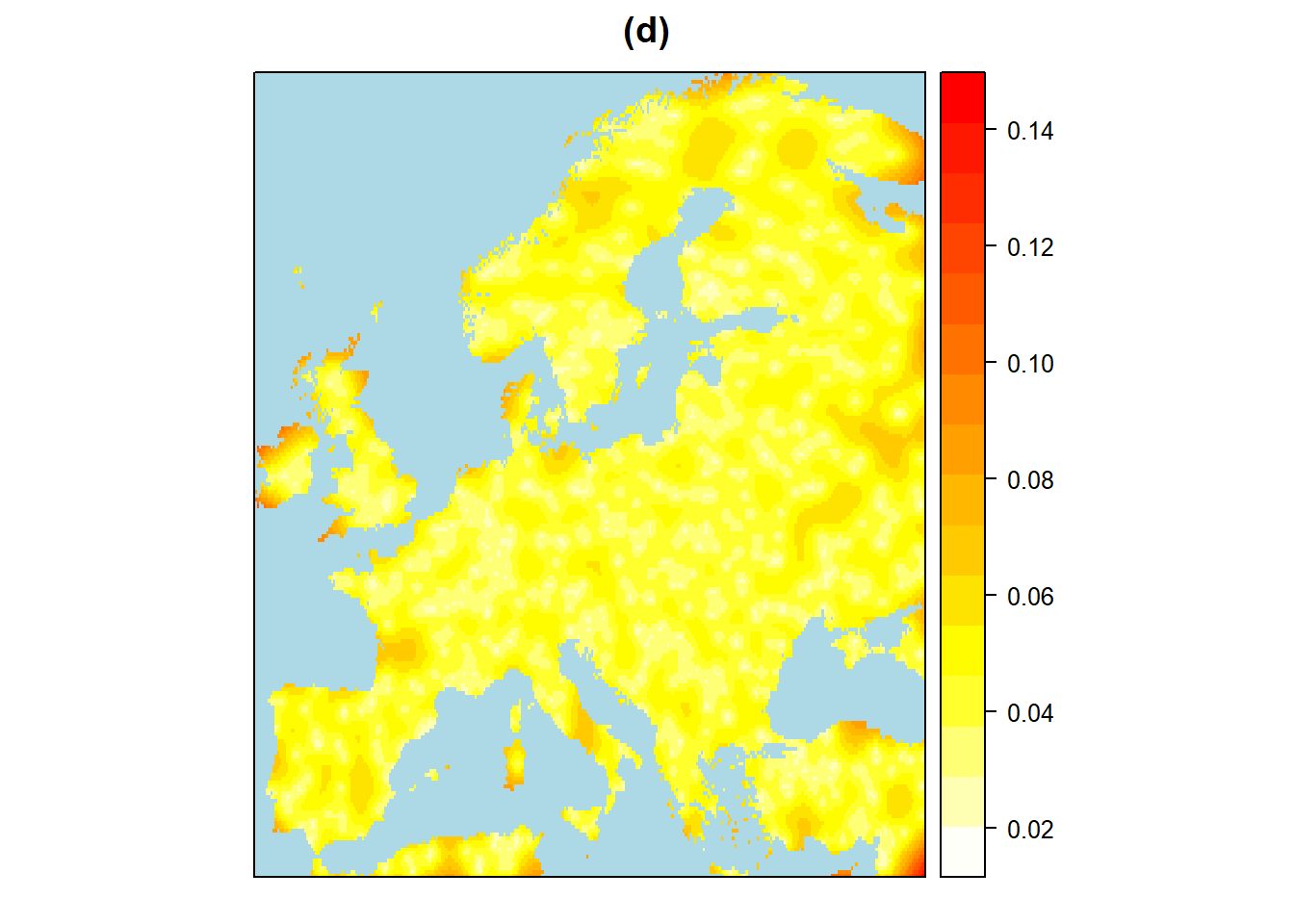
Figure 5: Interpolation Europaeische Risikogebiete für Niederschlagszunahmen und -abnahmen von mehr als 5% mit Hilfe von Kriging und Sphaerischen Viriogramm-Modellen. a: Schaetzer für Niederschlagszunahmen von mehr als 5%. b: Fehler für Niederschlagszunahmen von mehr als 5%. c: Schaetzer für Niederschlagsabnahmen von mehr als 5%. d: Fehler für Niederschlagsabnahmen von mehr als 5%.
Diskussion
Die Niederschläge insgesamt nehmen im Norden zu und im Süden ab. Dies ist wahrscheinlich hauptsächlich auf die Auswirkungen der globalen Erwärmung zurückzuführen. Die Temperatur in Norwegen stieg zwischen 1900 und 2008 um 0,9 °C (Climate Change in Norway, 2021). Die steigende Temperatur und das reichliche Wasserangebot des nahen Atlantiks führten zu einer raschen Verdunstung des Wassers und in der Folge zu einer Zunahme der Niederschläge. Die außergewöhnlich trockene Mittelmeerregion hingegen könnte mit der verstärkten Antizyklonen Zirkulation und der Nordverschiebung der atlantischen Sturmbahn zusammenhängen (Giorgi & Lionello, 2008). Darüber hinaus ein positiver NAO-Index kann auch dazu führen, dass in Nordeuropa mehr und im Mittelmeerraum weniger Niederschlag fällt (Bates et al., 2008). Gleichzeitig entspricht die Variation der Niederschlagsmenge eindeutig der Verteilung von Biomen. Dies kann durch topografische Faktoren beeinflusst werden. Zum Beispiel blockiert die skandinavischen Berge im Norden einen Teil der feuchten atlantischen Luftströmungen, wodurch die Niederschläge in dieser Region stärker zunehmen als in den umliegenden Gebieten.
Veränderungen bei den Niederschlägen können sich in mehrfacher Hinsicht negativ auswirken. Höhere Temperaturen und geringere durchschnittliche Niederschläge erhöhen die Wahrscheinlichkeit von Hitzewellen und Dürreperioden, die das Wachstum der Pflanzen beeinträchtigen können (Bates et al., 2008). Die Mittelmeerregion, in der bereits im Sommer wenig Niederschlag fällt, ist hoch brandgefährdet. In Regionen mit erhöhtem Niederschlagsrisiko erhöhen extreme Regenfälle die Wahrscheinlichkeit von Überschwemmungen und können in Ländern wie Norwegen, die auf Wasserkraft angewiesen sind, schwere Schäden verursachen. Darüber hinaus können sich auch Veränderungen bei den Niederschlägen auf die Qualität und Quantität des Wassers in Europa auswirken (Bates et al., 2008). Denn sowohl extreme Regenfälle als auch Dürreperioden können die Mikroorganismen im Wasser erhöhen, die wiederum Krankheiten verursachen können. Geringe Niederschläge im Mittelmeerraum könnte auch zum Verschwinden einiger kurzlebiger aquatischer Ökosysteme führen, während die biologische Vielfalt im Mittelmeerraum, einem sensiblen Gebiet für die biologische Vielfalt, ebenfalls stark beeinträchtigt werden könnte, wenn die Niederschläge weiter abnehmen (Newbold et al., 2020).
Die Niederschlagsverhältnisse in Europa haben sich in den letzten Jahrzehnten erheblich verändert. Zwischen der Zeiträumen 1962-1970 und 2010 bis 2018 hat der Jahresniederschlag in Europa in der nördlichen Tundra um 20 % zugenommen und in den südlichen Mittelmeerwäldern um 25 % abgenommen. Dies kann durch Faktoren wie die globale Erwärmung und die Topografie beeinflusst werden, die zu Katastrophen wie Dürren und Überschwemmungen führen können, mit negativen Auswirkungen auf die Landwirtschaft, die Energieversorgung, die menschliche Gesundheit und die biologische Vielfalt. Initiativen zur Bekämpfung des Klimawandels sind unerlässlich.
Literatur
Bates, B., Kundzewicz, Z. W., & IPCC (Eds.). (2008). Climate change and water.
Climate change in Norway. (2021). https://www.climatechangepost.com/norway/climate-change/
Dahlman, L. (2009). Climate variability: North atlantic oscillation | NOAA climate.gov. https://www.climate.gov/news-features/understanding-climate/climate-variability-north-atlantic-oscillation
Giorgi, F., & Lionello, P. (2008). Climate change projections for the Mediterranean region. Global and Planetary Change, 63(2-3), 90–104. https://doi.org/10.1016/j.gloplacha.2007.09.005
Newbold, T., Oppenheimer, P., Etard, A., & Williams, J. J. (2020). Tropical and Mediterranean biodiversity is disproportionately sensitive to land-use and climate change. Nature Ecology & Evolution, 4(12), 1630–1638. https://doi.org/10.1038/s41559-020-01303-0
Anhang
|
|